| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
Laboratorní cvičení TŘ – R3a, R3b
Výpočet frekvenční charakteristiky s využitím PC a její konstrukce, měření frekvenčních charakteristik
Zadání referátu:
Pro daný přenos soustavy 2. řádu, analyzované v prvním laboratorním cvičení, sestavte tabulku vypočítaných hodnot k sestrojení frekvenční charakteristiky.
Uveďte potřebné matematické vztahy a příklad výpočtu jednoho bodu frekvenční charakteristiky (pro jednu hodnotu frekvence).
Další body frekvenční charakteristiky řešte využitím programového vybavení na PC.
Frekvenční charakteristiku sestrojte:
a. v komplexní rovině
b. v logaritmických souřadnicích
Zkonstruujte asymptotické logaritmické frekvenční charakteristiky měřené soustavy a zpětně usuzujte na její vlastnosti.
Změřte
frekvenční charakteristiku ![]() na objektech:
na objektech:
a. Černá skříňka (fázový posuv určete kompenzační metodou)
b. Naměřená soustava 2. řádu (fázový posuv určete z Lissajousova obrazce – elipsy)
Naměřené frekvenční charakteristiky graficky znázorněte:
a. v komplexní rovině
b. v logaritmických souřadnicích
Z průběhu frekvenčních charakteristik určete:
a. řád soustavy
b. statické zesílení soustavy
Proveďte zhodnocení použitých metod a získaných výsledků.
Ad 1) Tabulka vypočtených hodnot:
Pro výpočet všech hodnot jsme využili podpůrný software vytvořený právě pro tuto praktickou úlohu.
|
f[Hz] | ||||||||||||
|
Re | ||||||||||||
|
Im | ||||||||||||
|
A[w] | ||||||||||||
|
A[dB] | ||||||||||||
|
ω [rad/s] |
Ad 2) Příklad výpočtu jednoho bodu frekvenční char.:
Pro výpočet frekvenční charakteristiky provedeme substituci p = jω :

Úprava na samostatnou reálnou a imaginární část:

Výpočet amplitudy obecně:

Dosazení konkrétních koeficientů našeho přenosu:

Ad 3)
a) Frekvenční charakteristika v komplexní rovině
Graf sestrojený z informací uvedených v tabulce (viz příloha č.3.).
b) Frekvenční charakteristika v logaritmických souřadnicích
Graf sestrojený jako ekvivalent charakteristiky v komplexní rovině. (viz příloha č.4.) Tak že zlogaritmujeme frekvenční přenos:
![]()
Zvlášť poté vyneseme logaritmus amplitudy (LAFCH) a zvlášť fázi (LFFCH). Na x osu vynášíme dekadický logaritmus kruhové frekvence. Pro tento postup se používá stupnice s dekádovým popř. oktávovým intervalem.
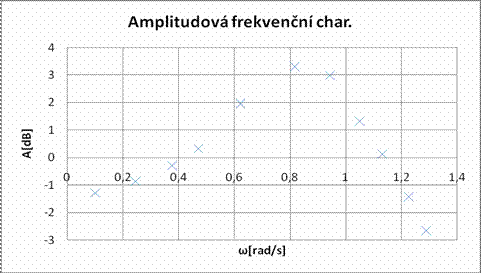
Amplitudová frekvenční charakteristika
Na svislou osu vynášíme tzv. zisk (dB)

Příklad dosazení:
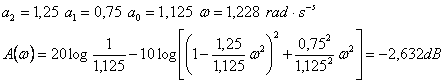
Ostatní potřebné hodnoty nalezneme v tabulce a graf proto můžeme sestrojit (viz příloha č.4 ).
Fázová frekvenční charakteristika
Na svislou osu fázové frekvenční charakteristiky vynášíme fázi (fázový posuv) Φ(ω) v úhlových stupních:
![]()
Příklad dosazení:

Ostatní hodnoty použijeme z tabulky a sestrojíme graf(viz příloha č.4.).
Ad 4) Asymptotické logaritmické frekvenční charakteristiky
a) Amplitudová frekvenční charakteristika(LAFCH)
(viz příloha č.5.)
Průběh naší amplitudové charakteristiky nahradíme asymptotickým průběhem.
Rovnice asymptoty pro 1° pro ω = 0 rad/s:

rovnice přímky rovnoběžná s osou x
Rovnice asymptoty pro 2° pro ω - ∞ rad/s:

rovnice přímky se sklonem -40 dB/dek a průsečík je dán společným řešením obou rovnic. Neboli stačí nám 2 body pro narýsování a nalezení průsečíku.Dosadím body ω1=0,9 rad/s a ω2=1.2 rad/s:
![]()
b) Fázová frekvenční charakteristika(LFFCH)
(viz příloha č.5.)
Opět nahradíme průběh fázové charakteristiky asymptotickým průběhem.
Rovnice asymptoty pro ω = 0 rad/s:
![]() = přímka
rovnoběžná s x v 0°
= přímka
rovnoběžná s x v 0°
Rovnice asymptoty pro ω = ωn ![]() rad/s:
rad/s:
 = přímka rovnoběžná s x v- 90°
= přímka rovnoběžná s x v- 90°
Rovnice asymptoty pro ω - ∞ rad/s:
 = přímka rovnoběžná s x v -180°
= přímka rovnoběžná s x v -180°
Na závěr spočteme činitel útlumu:

Ad 5) Frekvenční charakteristika
a) Černá skříňka (kompenzační metodou)
Měření jsme provedli
pomocí generátoru GNK (zapojení viz níže dle schématu), kde jsme nastavili
výstupní amplitudu na 4cm. Poté jsme měnili frekvenci ve vhodném rozsahu a
odečítali potřebné hodnoty amplitud z osciloskopu, kde jsme také
kompenzovali úhel ![]() a zapisovali do
tabulky. Zbylé hodnoty jsme spočítali pomocí vzorců:
a zapisovali do
tabulky. Zbylé hodnoty jsme spočítali pomocí vzorců:
![]()
![]()
![]()
![]()
![]()

|
f[Hz] | ||||||||||||
|
ω[rad/s] | ||||||||||||
|
A1[cm] | ||||||||||||
|
A2[cm] | ||||||||||||
|
rozsah G° | ||||||||||||
|
ϕ[rad] | ||||||||||||
|
A(ω) |
| |||||||||||
|
Re(jω) | ||||||||||||
|
Im(jω) | ||||||||||||
|
A[dB] |
b) Naměřená soustava druhého řádu
Pro tuto soustavu jsme si předem pomocí předloženého softwaru spočítali několik vhodných frekvencí pro následné vykreslení různě situovaných elips(viz příloha č.1. a č.2.). Z elips jsme následně odečtením a výpočtem získali fázový posun a ostatní části tabulky jsme vypočítali dle vzorců viz níže.

![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
|
f[Hz] | |||||||||||
|
2X | |||||||||||
|
2Y | |||||||||||
|
2y | |||||||||||
|
2x | |||||||||||
|
ϕ[rad] | |||||||||||
|
A(ω) | |||||||||||
|
A(dB) | |||||||||||
|
Re(jω) | |||||||||||
|
Im(jω) | |||||||||||
|
A(dB) |
Ad 6) Grafické znázornění
a) Černá skříňka



b) Naměřená soustava druhého řádu


AD 7) Z průběhu frekvenčních charakteristik určete:
a) Černá skříňka
Řád soustavy
Z frekvenční charakteristiky v komplexní rovině, kde prochází dvěma kvadranty zároveň z amplitudové frekvenční char. Zde klesá asymptoticky -40dB/dek a z průběhu fázové frekvenční charakteristiky,kde se úhel mění v intervalu od <0;-π> usuzujeme, že soustava je 2.ho řádu.
Statické zesílení soustavy
Statické zesílení jsme se snažili odečíst z grafu frekvenční charakteristiky v komplexní rovině, kde nám ovšem chybí zásadní hodnoty kde se imaginární složka blíží k nule a reálná složka k potencionálnímu statickému zesílení při nulové úhlové frekvenci. Proto můžeme jen usuzovat, že statické zesílením cca k=2.
b) Soustava 2.ho řádu
Řád soustavy
Jelikož o soustavě víme, že je 2.ho řádu, poté pouze ověřujeme její vlastnosti. Z výsledků můžeme usuzovat že splnila podmínky stejné jako u odhadu řádu černé skříňky a jedná se tedy o kmitavou statickou soustavu 2.ho řádu.
Statické zesílení soustavy 2.ho řádu
Z frekvenční charakteristiky
zakreslené v komplexní rovině odečteme statické zesílení pro
nulovou úhlovou rychlost a bude se rovnat reálné složce a ta je cca k=0,9. Pomocí kontrolního výpočtu
zjistíme, že odchylka je velmi malá: ![]()
Ad 9) Zhodnocení výsledků a závěr:
Příloha č.3.


Příloha č.4.



Příloha č.5



|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1800
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved